司雨萌 王相平 冯国全 2024年10月18日
随着航空发动机朝着高推重比、高转速方向发展,整机振动问题日益复杂,总结承力系统动态特性对发动机振动特性的影响规律,可以为航空发动机的设计及故障诊断工作提供支撑。
航空发动机整机振动问题是影响发动机可靠性的重要因素之一,严重地影响了发动机的研制、试验和使用[1-2]。航空发动机整机振动设计准则中阐述了,在技术设计阶段,如采用转子-支承系统的梁分析模型,则需在评估支承刚度时考虑支承系统动刚度的影响[3]。目前,国内大多数研究均采用不随频率变化的静刚度加载的方法,而有研究表明承力系统刚性并不是静态的,所以有必要考虑在机匣动柔度影响下的转子系统动力学特性。
航空发动机承力系统主要由进气机匣、压气机机匣、燃烧室机匣、尾喷管等结构组成[4]。其中,内、外机匣简化为考虑剪切变形的铁木辛柯梁,承力支板、轴承、拉杆、安装节等简化为刚度不变的弹簧单元,各部分将质量、转动惯量按照重心等效的原则分配到相关节点上,采用梁单元建立承力系统模型如图 1所示。
图1 承力系统简化模型 |
由于承力系统与转子系统一共有4个连接处,分别为1支点、2支点、3支点和5支点,所以运用有限元软件SAMCEF/ROTOR,在上述承力系统各支点位置上分别施加1N的简谐激振力进行谐响应分析[5],求解方法为完全法,定义频率范围为0~300Hz,求解个数为300个,计算各支点位置在简谐激励作用下的位移值,将计算结果绘制成1支点、2支点、3支点及5支点动柔度曲线,如图 2所示。
图2 支点动柔度曲线 |
图2中航空发动机承力系统动柔度随频率变化较为明显,不同支点的刚度特性有明显的差别。1支点、2支点、3支点及5支点动柔度均在91Hz、119Hz、132Hz、179Hz和240Hz附近出现峰值,对比固有频率计算结果,发现在机匣固有频率附近,动柔度急剧变化。各支点在100Hz、148Hz、170Hz左右动柔度值较小,在对发动机振动特性进行分析时,需关注上述频率范围,考虑承力系统对振动特性的影响。
将机匣、安装节、承力支板等结构考虑为支承系统在各支点上的动刚度来分析整机振动特性,建立简化航空发动机双转子系统的有限元计算模型。根据发动机结构特点,其中高、低压转子简化为考虑剪切变形的铁木辛柯梁,轴承简化为刚度不变的弹簧单元,各部分将质量、转动惯量按照重心等效的原则分配到相关节点上,计算模型共分2条线,5个弹簧,简化计算模型如图 3所示。
图3 双转子-支承系统简化模型 |
整机振动设计准则中提到在发动机技术设计阶段,可以采用静刚度的方法计算发动机振动特性,而在发动机详细设计阶段,如仍采用转子-支承系统的梁分析模型,则需在评估支承刚度时考虑支承系统动柔度的影响。由于静柔度难以描述动态特性对转子动力特性的影响,所以本文应用加载动柔度的方法来分析整机振动特性。
在有限元软件SAMCEF/ROTOR中通过建立表格函数的方法在各支点位置施加如图2对应的各支点动刚度值,定义频率范围为0~300Hz,考虑陀螺力矩的影响,计算该动刚度加载下的高压激振临界转速如表1所示,振型如图4所示。
表1 应用支承动柔度计算临界转速及应变能占比结果
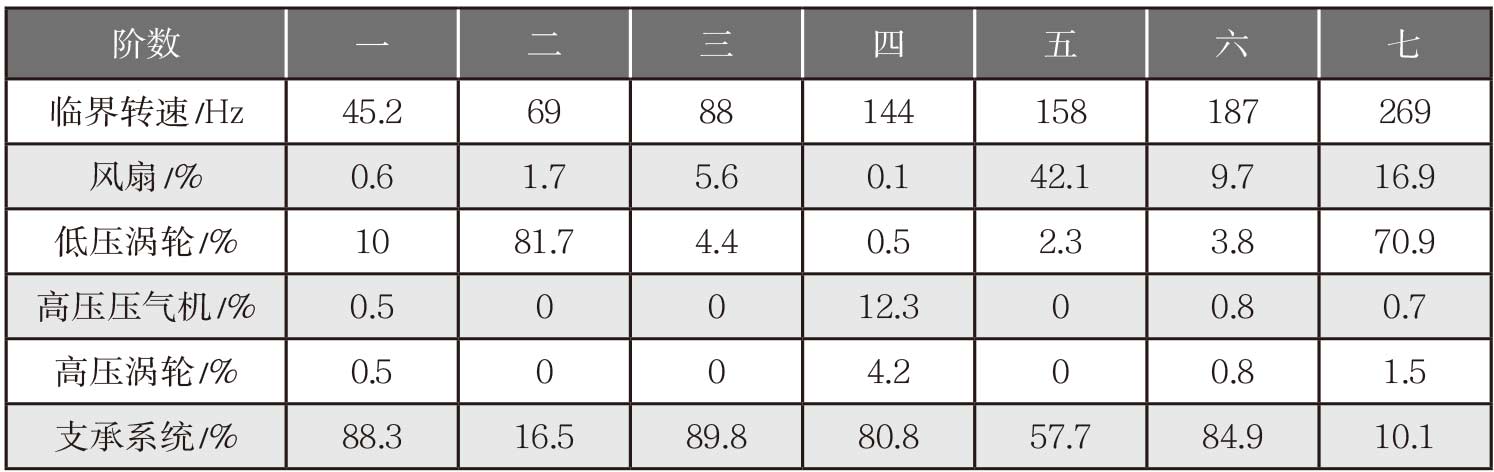
图4 高压激振振型 |
高压激振第一阶、第二阶、第三阶临界转速远低于高压慢车转速,高压应变能占比均小于1%,在满足平衡精度的前提下,起动时快速通过不会引起较大的振动。
高压激振第四阶临界转速为144Hz,振型为高压压气机俯仰模态,3支点变形最大,高压转子的应变能占比仅有16.7%,该阶临界转速较慢车转速具有20%以上的裕度,因此也不会引起较大振动。高压激振第五阶临界转速为158Hz,振型为风扇、涡轮转子俯仰模态,2支点变形最大;高压激振第六阶临界转速为187Hz,振型为风扇俯仰模态,高压转子应变能占比几乎为0,支承系统占比较大;高压激振第七阶临界转速为269Hz,振型为低压转子弯曲模态,高压转子应变能占比2.2%,低压转子应变能占比87.8%;此3阶临界转速的激振源是高压转子,但高压转子的应变能占比很小,所以在满足平衡精度的前提下,也不会引起较大的振动。
通过分析加载动柔度的双转子振型,从图4(c)和图 4(f)可知,高压激振转子第三阶振型与高压激振转子第六阶振型均为风扇俯仰模态,从表 1可以看出,这两阶中各部分应变能占比相似,支承系统应变能占比最大,其次为风扇转子。为探究出现第三阶与第六阶振型形式相似的原因,将该两阶应用动柔度的双转子振动特性计算结果与整机系统计算结果对比,如表 2所示。
表2 振动特性对比
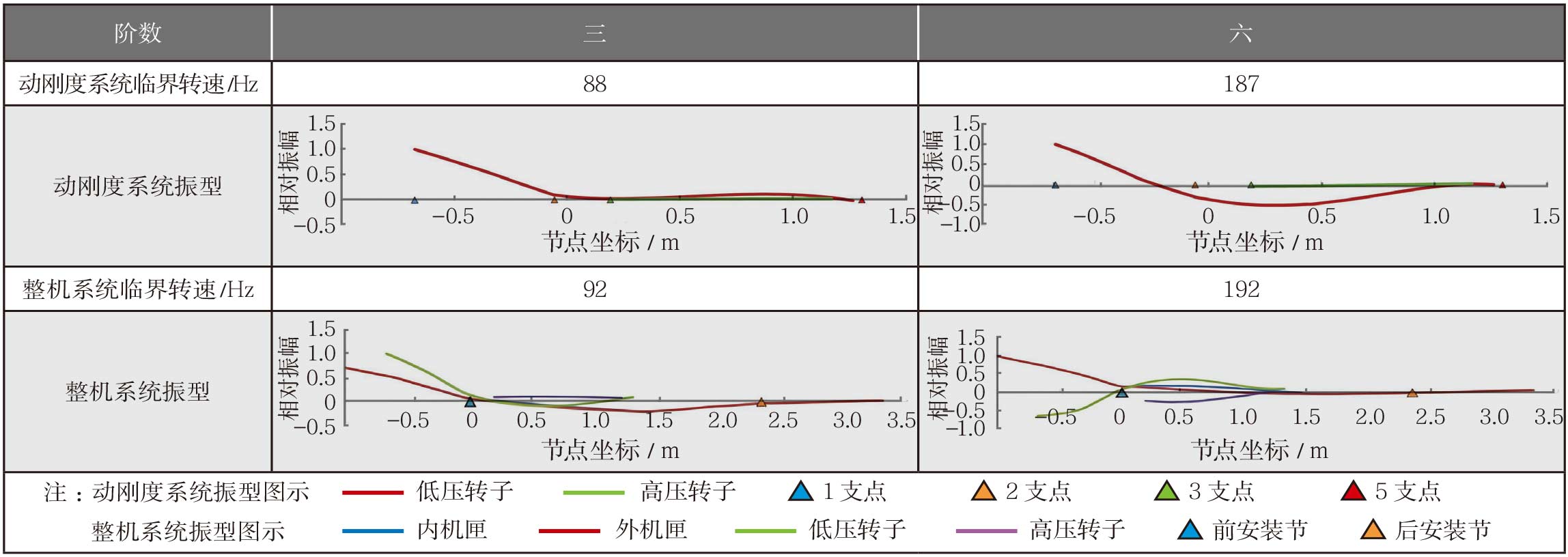
临界转速及振型方面,由表 2 振动特性对比可以看出,在运用整机模型分析时,同样出现了第三阶和第六阶振型相同的现象,但从整机系统振型中可以十分清楚地看出,在第三阶时,转子与机匣振动方向相同,而第六阶时,转子与机匣的振动方向相反,但对于转子来讲都属于风扇转子俯仰模态。所以,应用动柔度计算时之所以出现两阶振型相同的现象,是因为支承系统与转子间的耦合影响导致的转静子之间运动方向不同。总的来说,不论使用动柔度加载的双转子系统还是运用整机系统分析,该两阶临界转速及振型结果相似。
应变能方面,由图 5能量分布对比可以看出,第三阶与第六阶中加载动刚度的双转子系统与整机系统的各部件应变能分布相似,误差不超过5%,且均为支承系统应变能占比最大(在80%以上),其次为风扇转子(在5%以上)。
图5 能量分布对比 |
加载动柔度的双转子系统第三阶低压转子应变能占比为10%,高压转子应变能占比为0,高低压转子应变能占比之和为10%,支承系统应变能占比为89.8%,转静子之间应变能之比为0.11;整机系统中第三阶低压转子应变能占比为10.2%,高压转子应变能占比为0.2%,高低压转子应变能占比之和为10.4%,支承系统应变能占比为89.7%,转静子间应变能之比为0.12。可以明显看出两种分析模型的转静子间应变能之比高度相似。
加载动柔度的双转子系统第六阶低压转子应变能占比为13.5%,高压转子应变能占比为1.6%,高低压转子应变能占比之和为15.1%,支承系统应变能占比为84.9%,转静子之间应变能之比为0.17;整机系统中第六阶低压转子应变能占比为11.2%,高压转子应变能占比为1.8%,高低压转子应变能占比之和为13%,支承系统应变能占比为87%,转静子间应变能之比为0.15。在第六阶时两种模型计算的转静子应变能比例同样相似,可以充分判断加载动柔度的双转子系统计算方法较为准确。
通过对两种分析模型的应变能分析,进一步说明了加载动柔度的双转子系统可以体现出整机模型计算中的机匣与转子不同向的现象,且建模难度小、准确性高、临界转速及应变能对应情况良好,可以充分考虑到航空发动机承力系统对转子振动特性的影响。
在支承系统中承力支板起到支承的关键作用,为进一步研究支承系统动刚度的变化规律,通过改变各支点承力支板的刚度值来计算其对支承系统动柔度及固有频率的影响,更好地为后续应用动柔度来计算整机振动特性提供有力支撑。
在有限元软件SAMCEF/ROTOR中,改变1支点、2支点、3支点及5支点的承力支板刚度值,改变范围是1×107∼3×108N/m,计算支承系统固有频率变化曲线如图 6所示。
图6 支板刚度对固有频率的影响 |
由图 6可知,改变1支板刚度对支承系统前5阶固有频率影响不大,刚度值由3×107N/m变化到5×107 N/m,第六阶固有频率由283Hz变化到273Hz,变化率为3.6%,后续第六阶固有频率不再随刚度变化而变化;2支板刚度同样是在该变化区间,第六阶固有频率由271Hz变化到273Hz,变化率为0.7%,可以看出改变2支板的刚度对支承系统固有频率影响不大;3支板同样是在该变化区间,第五阶固有频率由203Hz变化到231Hz,变化率为12.5%,第六阶固有频率由257Hz变化到270Hz,变化率为4.8%,可以看出改变3支板的刚度对支承系统第五阶和第六阶固有频率影响较大。
5支板刚度对支承系统前6阶固有频率影响较大,5支板刚度从1×107N/m变化到3×107N/m,第一阶固有频率增加了3Hz,增大了3%,第二阶固有频率增加了2.7Hz,增大了2.2%,第三阶固有频率增加了12Hz,增大了10%,第四阶固有频率增加了60Hz,增大了31%,第五阶固有频率增加了3Hz,增大了1.2%,第六阶固有频率增加了2Hz,增大了0.7%;5支板刚度从3×107N/m变化到5×107N/m,前3阶固有频率变化不大,第四阶固有频率增加了30Hz,增大了15%,第五阶固有频率增加了14Hz,增大了5.8%,第六阶固有频率增加了10Hz,增大了3.6%;5支板刚度从5×107N/m变化到1×108N/m,前5阶固有频率变化不大,第六阶固有频率增加了16Hz,增大了5.6%。
综上所述,1支板、2支板、5支板刚度在3×107∼5×107N/m区间内对第四阶、第五阶、第六阶固有频率影响较大,影响率在3%~15%区间内,其中5支板刚度对第四阶固有频率影响最大。在采用动刚度加载计算振动特性的方法阶段,可以充分考虑承力支板刚度在该区间对固有频率的影响。
由图7可知,1支板刚度对1支点动柔度在0∼150Hz影响不大,在150~300Hz随着支板刚度的增加,动柔度值依次降低,峰值频率点略有退后;2支板刚度对2支点动柔度在0∼300Hz随着刚度值增加动柔度值依次降低;3支板刚度对3支点动柔度在0∼300Hz随着刚度值增加动柔度值依次降低,在180∼300Hz刚度值时,峰值频率点退后较多,刚度值从3×107N/m变化到1×108N/m时,峰值频率点变化不大;5支板刚度对5支点动柔度在0∼300Hz间随着刚度值增加动柔度值依次降低,在100∼300Hz刚度值从2×107N/m变化到5×107N/m时,峰值频率点退后较多,刚度值从1×108N/m变化到3×108N/m时,峰值频率点变化不大。
图7 支板刚度对动柔度的影响 |
综上所述,增大各支板刚度值,对应各支点的动柔度依次降低,在一定频段内,会产生固有频率增大(动柔度曲线峰值频率点后移)的现象。2支板刚度值对动柔度影响较小,可以忽略不计。
将应用动柔度的双转子-支承系统临界转速、振型及应变能结果与整机系统计算的临界转速、振型及应变能对比发现,相比于整机模型子结构多、建模难度大、计算时间长,应用动柔度的双转子-支承系统可以充分考虑机匣模态对转子临界转速的影响,也可以准确表达应变能分布规律。为航空发动机整机振动设计提供了一种切实可行的方法。
通过分析承力支板刚度对支承系统特性的影响发现,随着支板刚度的增加,各支点动柔度普遍下降,5支板刚度对支承系统固有频率影响最大,支承系统固有频率对5支板刚度在3×107∼5×107N/m内较为敏感,如需调整支承系统固有频率(或动柔度曲线峰值频率点)可以考虑改变5支板刚度,由于在发动机设计阶段是先设计转子再设计支承系统,那么对于先进发动机的整机振动设计而言都是采用以往的支承系统柔度经验值,本文给出调整动柔度及固有频率的方法,可以为后续使用动柔度加载的方法进行整机振动设计提供支撑。
(司雨萌,中国航发沈阳发动机研究所,硕士研究生,主要从事航空发动机整机振动研究)
参考文献
[1] ZORZI E S, NELSON H D. Finite element simulation of rotor bearing systems with internal damping[J]. ASME, 1977,99(1): 71-76.
[2] 任兴民.航空发动机整机动力特性分析方法研究[D].西安:西北工业大学,1999.
[3] 冯国全.航空发动机承力系统试验建模技术研究[J].航空发动机,2005(4):30-31+5.
[4] 赵文涛,陈果,李琼,等.航空发动机机匣支承动刚度有限元计算及验证[J].航空计算基数,2011,41(5):34-38+41.
[5] 赵文涛.考虑实测支承动刚度的航空发动机整机振动建模及验证[D].南京:南京航空航天大学,2012.
《航空动力》期刊由中国航空发动机集团有限公司主管、中国航空发动机研究院主办,《航空动力》编辑部出版。国内统一连续出版物号为 CN10-1570/V;国际标准连续出版物号为 ISSN 2096-5702;邮发代号为82-467;广告发布登记号为京顺工商广告登字20190001号 。
关注世界航空发动机前沿动态,反映国内外航空发动机管理与技术创新成果,传播航空发动机知识与文化,促进我国航空发动机自主创新能力的提升。
《航空动力》设有专稿、综述、技术、管理、市场、维修、动态等主要栏目,每期还围绕航空发动机及燃气轮机在技术、管理等方面的新理论和新方法策划相应的专题。
《航空动力》面向航空发动机及燃气轮机领域的决策、管理、科研、生产、使用、维护的专业人士,高校师生,以及关注航空发动机及燃气轮机事业发展的热心人士。
《航空动力》所刊登的文章密切跟踪世界航空动力、燃气轮机领域的最新科技动态,准确把握发展规律,权威预测发展趋势,及时展示创新成果,为科研和管理工作提供支撑。
以Word文件格式,发送至:
tg@aerospacepower.cn
请在邮件主题中注明:
《航空动力》投稿+作者姓名+联系电话
地址:北京市顺义区顺兴路21号
邮编:101304
电话:010-56680887
网址:https://www.aerospacepower.cn
本刊享有以数字化方式复制、汇编、发行并由互联网传播所刊载文章的权利,相关著作权使用费均包含在本刊一次性支付的稿酬中。作者向本刊投稿,即视为同意我刊上述声明。如有特殊要求,请在投稿时声明。未经本刊书面授权擅自使用上述版权作品之个人、机构或媒体,均属侵犯本刊合法权益,本刊保留依法追究的权利。
ICP备案/许可证编号:京ICP备18031095号
《航空动力》编辑部 版权所有